Подъёмная сила. Статический вариант.
А все просто - ничего не будет, в смысле подъемной силы не будет. Будет большее давление сверху, и Ваша лопасть никуда не “улетит”. Смысл описывать разность давлений, когда есть разделение одного потока на два, тогда за счет разности скорости отекания сверху снижается давление. А в Вашем случае - это один поток сверху, который давит на поверхность. Профильните деревянную линейку с одной стороны, положите ее на стол и дуйте вентилятором вдоль плоскости стола. Когда линейка взлетит - отчитайтесь в этой теме о величине подъемной силы, полученной экпериментальным путем.
вы ошибаетесь
просто дуть нужно с другой стороны
И, кстати, некоторые расспрыскиватели, в частности смесители в карбюраторах именно на таком “статическом” принципе работают (когда воздух дует только с одной стороны), на сколько понимаю.
например труба Вентури
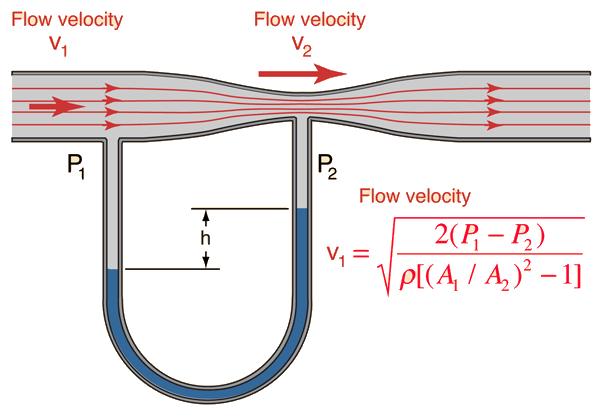
Да.
Кто-нибудь может сказать какой характерный порядок величин для коэффициента подъёмной силы (будь то для лопасти или крыла) поточнее, нежели, чем это сказано в Википедии?
Эта ссылка у меня что-то не открывается.
попробуйте тут
Спасибо! Но что-то никак не соображу: там зачем-то экспериментировали с симметричными (т.е. каплевидными) крыльями. Мне всегда казалось, что подъёмная сила у крыла (или лопасти) создаётся, главным образом, за счёт разности скоростей потока сверху и снизу, которая возникает за счёт того, что профиль крыла сверху - более выпуклый, чем снизу. А они, почему-то экспериментировали с симметричным профилем и подъёмная сила у них, тогда получается, создавалась только благодаря не нулевого угла атаки.
А они, почему-то экспериментировали с симметричным профилем и подъёмная сила у них, тогда получается, создавалась только благодаря не нулевого угла атаки
ну они много с чем экспериментируют 😃
зато получили зависимость в чистом виде
Интересно, сколько процентов энергии идёт на преодоление лобового сопротивления для типичного профиля крыла? Хотелось бы сообразить на сколько эффективнее или не эффективнее будет использовать для создания подъёмной силы выше описанный статичный вариант. В нём, получается, лобовое сопротивление равно нулю. Но, может, коэффициент подъёмной силы будет чуть поменьше. Собственно, поэтому и спрашивал про его типичное значение, а не для не реального (т.е. не используемого на практике) случая каплевидной формы профиля крыла/лопасти.
Вы имеете в виду воспользоваться тем, что ro*v^2/2 + p = ro*V^2/2 + P ?
Где v, p - скорость и давления над крылом, V, P - под крылом. И, поскольку, по исходному предположения, под крылом скорость равна нулю, а давление - атмосферное, то отсюда получается давление над крылом p=P-ro*v^2/2. Ну , соответственно, для подъёмной силы получается (P-p)*s = ro*v^2/2 , где s - площадь.
Хм … вроде, просто, банально … удивляюсь как сам не догадался …
Теперь мне кажется, что в этих расчётах ошибка: ведь формула ro*v^2/2 + p = ro*V^2/2 + P, кажись, работает лишь для непрерывной “трубки” потока. Тогда как “под” и “над” крылом - это будут разные трубки … А … ну, хотя же, наверно, можно себе представить, что где-то на бесконечности они соединяются … как-то раньше не задумывался и сохраняется какая-то неуверенность …
Тогда как “под” и “над” крылом - это будут разные трубки
почему разные?
Закон Бернулли действует для непрерывных сред. И не важно трубка это или бассейн.
Представьте, что мы заменяем воздух жидкостью, она непрерывна и “соединяет” области над крылом и под ним.