Подъёмная сила. Статический вариант.
Имеет смысл рассматривать данный параметр в зависимости от угла атаки.
Например вот тут хорошо описано
Интересно, существует ли угол атаки, при котором достигается наибольшая эффективность в создании подъёмной силы (имеется в виду до угла срыва)? Под эффективностью имеется в виду подъёмная сила, приходящаяся на единицу мощности. Или эффективность от угла атаки, в некоторых практических пределах (до угла срыва) зависит очень слабо?
Под эффективностью имеется в виду подъёмная сила, приходящаяся на единицу мощности
О как!
Рекомендую почитать ветку про хвост
В частности там приводили ссылку на статью наса
За силу относящуюся к единице мощности не скажу, но сама сила, в интересующем диапазоне, растет практически линейно.
Имеет смысл рассматривать данный параметр в зависимости от угла атаки.
Например вот тут хорошо описано
Ну у вертолётов же коэффициент подъёмной силы, наверно, обычно, очень близок к единице?
Ну у вертолётов же коэффициент подъёмной силы, наверно, обычно, очень близок к единице?
с вертолетом не все так просто
коэффициент будет меняться по длине лопасти
Ну а если примерно? Пытаюсь хотя бы ориентировочно понять что будет лучше/хуже по эффективности расходования мощности на создания единицы подъёмной силы и на сколько: просто дуть вдоль поверхности (плоского крыла), создавая подъёмную силу или двигать крыло (например, как у вертолёта) вдоль воздуха.
Ну а если примерно?
примерно не получится.
в центре (ось вращения) будет ноль
ближе к концу лопасти (максимальный радиус) будет максимум - опять же условно, так как очень много “если”
ну а между ними будет какой-то профиль… и далеко не линейный
двигать крыло (например, как у вертолёта) вдоль воздуха.
не совсем корректная модель.
двигать крыло - это самолет
а вот вращать лопасть - это вертолет, и это уже совсем другая история.
вот тут гляньте
Что касается “расходования мощности” тоже не понятно как сравнивать. Ведь для того чтобы “двигать крыло” и “дуть вдоль поверхности” нужны принципиально разные “мощности”.
И что-то мне подсказывает, что создавать поток воздуха (дуть вентилятором) будет гораздо затратнее, чем просто двигать крыло.
примерно не получится.
в центре (ось вращения) будет ноль
ближе к концу лопасти (максимальный радиус)
Да ну: что-то не то. Коэффициент пропорциональности между подъёмной силой и квадратом скорости у лопасти, по-моему, нигде не может быть равным нулю. Мне кажется, что Вы говорите о какой-то другой величине. Подъёмная сила при нулевом радиусе будет равна нуля - это да. Но это не значит, что упомянутый коэффициент будет равен нулю. Я же про него спрашивал, а не про удельную (на единицу площади лопасти) подъёмную силу. Ну хорошо: будем речь вести не о суммарной подъёмной силе лопасти вертолёта, а об удельной - на единицу площади. Формула для неё имеет вид: k*ro*v^2/2 . Где v зависит от радиуса. Но k, по идее, нет. Каков порядок этой величины для вертолёта знаете, нет?
Что касается “расходования мощности” тоже не понятно как сравнивать. Ведь для того чтобы “двигать крыло” и “дуть вдоль поверхности” нужны принципиально разные “мощности”.
И что-то мне подсказывает, что создавать поток воздуха (дуть вентилятором) будет гораздо затратнее, чем просто двигать крыло.
Можно не обязательно дуть вентилятором. Можно, например, качать поршнем.
Каков порядок этой величины для вертолёта знаете, нет?
у вертолета этот коэффициент также будет меняться по длине из-за продольного изгиба и крутки лопасти
порядок величины (без учета этих и других явлений) можно взять из стать наса для самолета, ссылку давал выше.
Можно не обязательно дуть вентилятором. Можно, например, качать поршнем.
даже если брать двухходовой поршень, то потери на трение у стенки будут выше.
у вертолета этот коэффициент также будет меняться по длине из-за продольного изгиба и крутки лопасти
порядок величины (без учета этих и других явлений) можно взять из стать наса для самолета, ссылку давал выше.
Эта ссылка у меня что-то не открывается.
даже если брать двухходовой поршень, то потери на трение у стенки будут выше.
Это смотря какой поршень делать. Можно сделать так, что у стенки трения вообще почти не будет. Грубо говоря, что-то вроде этого: dailytechinfo.org/…/4322-pezoelektricheskie-sistem…
Lesha 74: “Интересно, а какова будет формула для подъёмной силы, если воздух будет двигаться только “над” и будет иметь нулевую скорость “под”. Получается статичный случай типа дующего ветра вдоль плоской крыши дома с данной скоростью.”
А все просто - ничего не будет, в смысле подъемной силы не будет. Будет большее давление сверху, и Ваша лопасть никуда не “улетит”. Смысл описывать разность давлений, когда есть разделение одного потока на два, тогда за счет разности скорости отекания сверху снижается давление. А в Вашем случае - это один поток сверху, который давит на поверхность. Профильните деревянную линейку с одной стороны, положите ее на стол и дуйте вентилятором вдоль плоскости стола. Когда линейка взлетит - отчитайтесь в этой теме о величине подъемной силы, полученной экпериментальным путем.
А все просто - ничего не будет, в смысле подъемной силы не будет. Будет большее давление сверху, и Ваша лопасть никуда не “улетит”. Смысл описывать разность давлений, когда есть разделение одного потока на два, тогда за счет разности скорости отекания сверху снижается давление.
Разность давления возникает не за счёт разделения потока на два, а за счёт того, что они имеют разную скорость. Чем больше скорость - тем меньше давление. Т.к. сверху скорость получается выше (из-за формы крыла или лопасти, то там скорость получается выше, а давление - ниже) Посмотрите закон Бернулли. И, кстати, некоторые расспрыскиватели, в частности смесители в карбюраторах именно на таком “статическом” принципе работают (когда воздух дует только с одной стороны), на сколько понимаю.
А все просто - ничего не будет, в смысле подъемной силы не будет. Будет большее давление сверху, и Ваша лопасть никуда не “улетит”. Смысл описывать разность давлений, когда есть разделение одного потока на два, тогда за счет разности скорости отекания сверху снижается давление. А в Вашем случае - это один поток сверху, который давит на поверхность. Профильните деревянную линейку с одной стороны, положите ее на стол и дуйте вентилятором вдоль плоскости стола. Когда линейка взлетит - отчитайтесь в этой теме о величине подъемной силы, полученной экпериментальным путем.
вы ошибаетесь
просто дуть нужно с другой стороны
И, кстати, некоторые расспрыскиватели, в частности смесители в карбюраторах именно на таком “статическом” принципе работают (когда воздух дует только с одной стороны), на сколько понимаю.
например труба Вентури
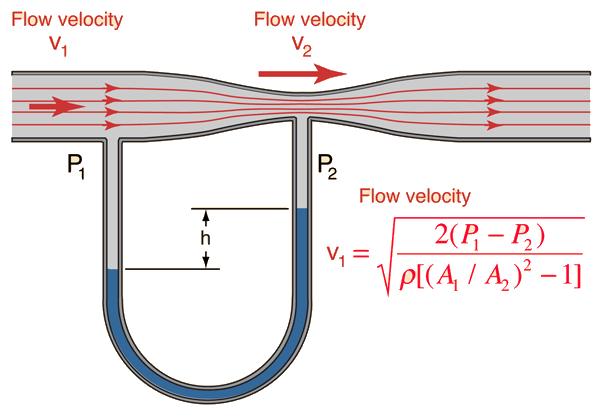
Да.
Кто-нибудь может сказать какой характерный порядок величин для коэффициента подъёмной силы (будь то для лопасти или крыла) поточнее, нежели, чем это сказано в Википедии?
Эта ссылка у меня что-то не открывается.
попробуйте тут
Спасибо! Но что-то никак не соображу: там зачем-то экспериментировали с симметричными (т.е. каплевидными) крыльями. Мне всегда казалось, что подъёмная сила у крыла (или лопасти) создаётся, главным образом, за счёт разности скоростей потока сверху и снизу, которая возникает за счёт того, что профиль крыла сверху - более выпуклый, чем снизу. А они, почему-то экспериментировали с симметричным профилем и подъёмная сила у них, тогда получается, создавалась только благодаря не нулевого угла атаки.
А они, почему-то экспериментировали с симметричным профилем и подъёмная сила у них, тогда получается, создавалась только благодаря не нулевого угла атаки
ну они много с чем экспериментируют 😃
зато получили зависимость в чистом виде
Интересно, сколько процентов энергии идёт на преодоление лобового сопротивления для типичного профиля крыла? Хотелось бы сообразить на сколько эффективнее или не эффективнее будет использовать для создания подъёмной силы выше описанный статичный вариант. В нём, получается, лобовое сопротивление равно нулю. Но, может, коэффициент подъёмной силы будет чуть поменьше. Собственно, поэтому и спрашивал про его типичное значение, а не для не реального (т.е. не используемого на практике) случая каплевидной формы профиля крыла/лопасти.
Вы имеете в виду воспользоваться тем, что ro*v^2/2 + p = ro*V^2/2 + P ?
Где v, p - скорость и давления над крылом, V, P - под крылом. И, поскольку, по исходному предположения, под крылом скорость равна нулю, а давление - атмосферное, то отсюда получается давление над крылом p=P-ro*v^2/2. Ну , соответственно, для подъёмной силы получается (P-p)*s = ro*v^2/2 , где s - площадь.
Хм … вроде, просто, банально … удивляюсь как сам не догадался …
Теперь мне кажется, что в этих расчётах ошибка: ведь формула ro*v^2/2 + p = ro*V^2/2 + P, кажись, работает лишь для непрерывной “трубки” потока. Тогда как “под” и “над” крылом - это будут разные трубки … А … ну, хотя же, наверно, можно себе представить, что где-то на бесконечности они соединяются … как-то раньше не задумывался и сохраняется какая-то неуверенность …
Тогда как “под” и “над” крылом - это будут разные трубки
почему разные?
Закон Бернулли действует для непрерывных сред. И не важно трубка это или бассейн.
Представьте, что мы заменяем воздух жидкостью, она непрерывна и “соединяет” области над крылом и под ним.