Головоломки, задачки и прочее
А если мы для начала посмотрим что будет если взять скажем 3 вместо 6. Очевидно что в этом случае улитка сможет проползти 4 метра. А 4 это как раз 2*(3-1)…
Вобщем, что-то мне кажется что она как раз 10 и проползет.
А вообще, какая-то тягучая задача… как ползущая улитка:)
Вопрос: а ответ должен получиться ЦЕЛЫМ? такое впечатление, что да. А тогда…Не, хорошая задача!)))
В 6-ти минутах не может быть более чем 2* (6-1)=10 наблюдателей, удовлетворяющих поставленным условиям.
В такой формулировке утверждение неверно.
Смотрите берем 25 наблюдателей первый из которых начинет в момент 0 каждый следующий до 20 включительно начинает через секунду от предыдущего
В - 0:00; 0:01; 0:02; 0:03; 0:04 ;0:05; 0:06; 0:07; 0:08; 0:09; 0:10; 0:11; 0:12; 0:13; 0:14; 0:15; 0:16; 0:17; 0:18; 0:19.
Все остальне наблюдатели начинают ровно в начале очередной минуты друг за другом.
21 начинает в 1:00 пересекаясь с первыми 20 в течении своей минуты с 1:00 по 1:19. и с 22 в 2:00
22 начинает в 2:00 пересекаясь с 21 в 2:00 и 23 в 3:00
…
25 начинает в 5:00.
В этой конфигурации начиная с 0:19 и до 1:00 за улиткой наблюдает 20 человек одновременно .
Начиная с 1:19 за исключением моментов 2:00, 3:00, 4:00, 5:00 за улиткой наблюдает один наблюдатель.
Улитка полезет ровно метр ровно в середине каждой минуты
В - 0:30, 1:30, 2:30, 3:30, 4:30, 5:30 - всего 6 метров
При этом все 25 наблюдателей каждый со своим интерваломи наблюдения, наблюдая минуту ровно увидит что улитка проползла ровно метр.
Первые 20 увидят метр пройденый в 0:30 остальные 5 каждый свой метр в середине их минуты.
Условие наблюдение выполнено для 25 наблюдателей. Этот пример опровергает утверждение в цитате и доказательство на его основе
WBR CrazyElk.
p.S. Требуется доказать что и 10 метров улитка проползти не может.
Вопрос: а ответ должен получиться ЦЕЛЫМ?
Ну скажем так - Мое доказательство базируется на определении точной верхней грани достижимой улиткой дистанции. Конструктивно она у меня целое число метров
Можно предьявить конфигурацию наблюдателей и алгоритм движения ее обеспечивающий + некотрые утверждения/выводы обосновывающие что изменение этой конфигурации или не изменит или уменьшит максимально возможную для улитки дистанцию
Ну а из значения моей оценки необходимое утверждение следует непосредственно.
Вот эта конфигурация по-моему доказывает что 10 достижимо:
отрезки:
0.0-1.0 0.15-1.15 1.10-2.10 1.25-2.25 2.2-3.2 2.5-3.5 3.4-4.4 3.75-4.75 4.6-5.6 5.0-6.0
точки прыжков улитки на 1м:
0.0 1.05 1.2 2.15 2.35 3.35 3.6 4.5 4.85 6.0
А если мы для начала посмотрим что будет если взять скажем 3 вместо 6. Очевидно что в этом случае улитка сможет проползти 4 метра.
А предьявите эти 4 очевидных метра котрые улитка сможет на интервале 3 минуты.
У меня как то не получается. 3 метра есть комбинация (тривиальная) а 4 никак не вытанцовыается.
WBR CrazyElk
P.S. И формула моя совсем другая не 2*(n-1).
А предьявите эти 4 очевидных метра котрые улитка сможет на интервале 3 минуты.
Ну как! Точки: две в концах интервала, и 2 рядом в середине; 2 отрезка примыкающие к концам интервала, и еще два “захватывающие” по одной “средней” точке и “сцепленные” между собой.
(ну я для 6 выше написал уже…))))
А я вот нашел сегодня эту задачку в Кванте 😃
Ход моих мыслей был схож.
www.problems.ru/view_problem_details_new.php?id=73…
Вот эта конфигурация по-моему доказывает что 10 достижимо:
Cильно думаю.
Ну как! Точки: две
А я вот нашел сегодня эту задачку в Кванте
give Up
Нашел в своих расуждениях и оценке ошибку.
Выкинуть полностью перекрытых догадался, разделить на четных и нечетных не перекрывающихся по по своей подгруппе догадался. Нечетных оценил верно, а с четным не учел одну из границ и в итоге ошибся (не засчитал) 1 интервал и получил формулу не 2*(t-1) а 2t-3 что поделать ЛОХ 😃.
Но задача все равно красивая.
Хи, таки две ошибки сделал… 😃
news.mail.ru/society/25976308/?frommail=10
две ошибки сделал…
тоже))
Хи, таки две ошибки сделал…
Попробуйте тут
www.kommersant.ru/doc/2999498
Задача:
На плоскости нарисована замкнутая линия. Всегда ли можно найти на ней 3 точки, чтобы они являлись вершинами правильного треугольника?
Думаю, что да.
Думаю, что да.
А 4 точки (квадрат)?))
Задача:
На плоскости нарисована замкнутая линия. Всегда ли можно найти на ней 3 точки, чтобы они являлись вершинами правильного треугольника?
А 4 точки (квадрат)?))
Всегда, если эта замкнутая линия - круг… и не всегда, если замкнутая линия нечто другое.
Ибо ПРАВИЛЬНЫЙ треугольник и квадрат это фигуры с центральной симметрией (центра́льной инве́рсией)
😎
Геометрические задачи
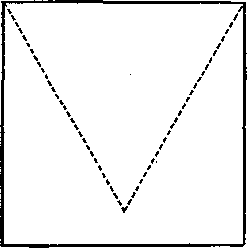
Возьмите квадратный лист бумаги и сложите его таким образом, чтобы получился наибольший из возможных равносторонний треугольник. Треугольник на рисунке, у которого все стороны равны стороне квадрата, не будет наибольшим. Разумеется, при этом производить измерения и пользоваться какими-либо инструментами не следует.
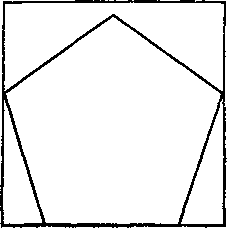
Если у вас имеется квадратный лист бумаги, то как следует его согнуть, чтобы сгибы образовали правильный пятиугольник (см. рисунок)? Сделать это вы должны «голыми руками», не прибегая к измерениям и инструментам.
вот еще
Ну это совсем старо. Гипотенуза треугольника не прямая.
Линейку к монитору прикладывали ? )))
Линейку к монитору прикладывали ? )))
Когда знаешь то и на глаз видно. А вообще по клеточкам если сравнивать то понятно становится.
Линейку к монитору прикладывали ? )))
😃
По клеточкам вычисляете тангенсы углов красного и тёмнозелёного треугольников.
Видите, что они - разные
Кажется предложенная мной задача не вызвала большого интереса, но (для порядка) все ж дам решение. (А то может подумали что это шутка была…))
Ответ - утвердительный: можно всегда построить равносторонний треугольник. Доказательство:
- В качестве первой вершины “А” берем произвольную точку на кривой.
- Равнобедренный треугольник найти легко: какую бы мы не взяли точку В на кривой, всегда найдется точка С такая что треугольник АВС равнобедренный (АС=ВС). Действительно, пусть точки А и В некоторые точки на кривой. Если взять точку С очень близко к А,то будет наверняка АС < ВС. Если взять С около В, то наоборот - АС > ВС. Двигая точку С от А к В вдоль кривой, в какой-то момент обязательно окажется АС = ВС.
- Теперь осталось найти такую точку В, для которой равнобедренный треугольник построенный в п.2 оказался бы еще и равносторонним. Идея та же что и в п.2. : двигаем В от А до А вдоль кривой и каждый раз строим равнобедренный треугольник АВС. Хотя бы один из них окажется равносторонним.
p.s. На тот же вопрос с четырьмя точками (квадратом), похоже ответа не знает никто…😮