Головоломки, задачки и прочее
А я вот нашел сегодня эту задачку в Кванте 😃
Ход моих мыслей был схож.
www.problems.ru/view_problem_details_new.php?id=73…
Вот эта конфигурация по-моему доказывает что 10 достижимо:
Cильно думаю.
Ну как! Точки: две
А я вот нашел сегодня эту задачку в Кванте
give Up
Нашел в своих расуждениях и оценке ошибку.
Выкинуть полностью перекрытых догадался, разделить на четных и нечетных не перекрывающихся по по своей подгруппе догадался. Нечетных оценил верно, а с четным не учел одну из границ и в итоге ошибся (не засчитал) 1 интервал и получил формулу не 2*(t-1) а 2t-3 что поделать ЛОХ 😃.
Но задача все равно красивая.
Хи, таки две ошибки сделал… 😃
news.mail.ru/society/25976308/?frommail=10
две ошибки сделал…
тоже))
Хи, таки две ошибки сделал…
Попробуйте тут
www.kommersant.ru/doc/2999498
Задача:
На плоскости нарисована замкнутая линия. Всегда ли можно найти на ней 3 точки, чтобы они являлись вершинами правильного треугольника?
Думаю, что да.
Думаю, что да.
А 4 точки (квадрат)?))
Задача:
На плоскости нарисована замкнутая линия. Всегда ли можно найти на ней 3 точки, чтобы они являлись вершинами правильного треугольника?
А 4 точки (квадрат)?))
Всегда, если эта замкнутая линия - круг… и не всегда, если замкнутая линия нечто другое.
Ибо ПРАВИЛЬНЫЙ треугольник и квадрат это фигуры с центральной симметрией (центра́льной инве́рсией)
😎
Геометрические задачи
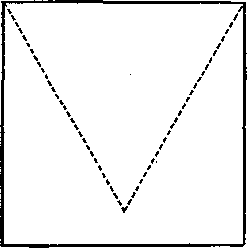
Возьмите квадратный лист бумаги и сложите его таким образом, чтобы получился наибольший из возможных равносторонний треугольник. Треугольник на рисунке, у которого все стороны равны стороне квадрата, не будет наибольшим. Разумеется, при этом производить измерения и пользоваться какими-либо инструментами не следует.
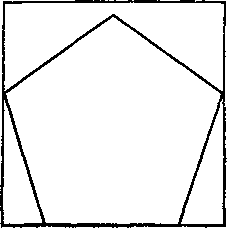
Если у вас имеется квадратный лист бумаги, то как следует его согнуть, чтобы сгибы образовали правильный пятиугольник (см. рисунок)? Сделать это вы должны «голыми руками», не прибегая к измерениям и инструментам.
вот еще
вот еще
Ну это совсем старо. Гипотенуза треугольника не прямая.
Линейку к монитору прикладывали ? )))
Линейку к монитору прикладывали ? )))
Когда знаешь то и на глаз видно. А вообще по клеточкам если сравнивать то понятно становится.
Линейку к монитору прикладывали ? )))
😃
По клеточкам вычисляете тангенсы углов красного и тёмнозелёного треугольников.
Видите, что они - разные
Кажется предложенная мной задача не вызвала большого интереса, но (для порядка) все ж дам решение. (А то может подумали что это шутка была…))
Ответ - утвердительный: можно всегда построить равносторонний треугольник. Доказательство:
- В качестве первой вершины “А” берем произвольную точку на кривой.
- Равнобедренный треугольник найти легко: какую бы мы не взяли точку В на кривой, всегда найдется точка С такая что треугольник АВС равнобедренный (АС=ВС). Действительно, пусть точки А и В некоторые точки на кривой. Если взять точку С очень близко к А,то будет наверняка АС < ВС. Если взять С около В, то наоборот - АС > ВС. Двигая точку С от А к В вдоль кривой, в какой-то момент обязательно окажется АС = ВС.
- Теперь осталось найти такую точку В, для которой равнобедренный треугольник построенный в п.2 оказался бы еще и равносторонним. Идея та же что и в п.2. : двигаем В от А до А вдоль кривой и каждый раз строим равнобедренный треугольник АВС. Хотя бы один из них окажется равносторонним.
p.s. На тот же вопрос с четырьмя точками (квадратом), похоже ответа не знает никто…😮
p.s. На тот же вопрос с четырьмя точками (квадратом), похоже ответа не знает никто…
при сторонах квадрата стремящихся к нулю, почему бы и нет?
Двигая точку С от А к В вдоль кривой, в какой-то момент обязательно окажется АС = ВС.
А по строже. Почему?
Пусть первое утверждение верно для любой на перед заданной точек А и произвольно выбранной на кривой точке B гарантированно найдется точка С такая что они образуют равнобедренный треугольник ABC ( [A,С]=[B,C]) .
Откуда следует что для конкреной точке A и стремлении к ней точки B (по кругу) найдется хоть один треугольник такой что [A,С]=[B,C]=[A,B]?
Для случае специально выбранной кривой и точки А на ней могу легко предьявить пример когда ни какой из треугольников построенный на замкнутой кривой с данной вершиной А не будет равносторонний. Как бы мы ни выбирали B и сколко бы мы не строили равнобедренных треугольников подбирая С.
“Пример”
Замкнутая кривая это остроугольный треугольник с одним из углов 15 градусов. Точка А вершина этого угла. Как бы мы ни выбирали точки C и B угол при вершине А не может быть больше этих самых 15 градусов, а значить треугольник не может быть равностронним.
Это не говрит что нельзя построить равностронний треугольник по другому выбрав точку А но это и не говорит что всегда можно выбрать точку А такую что один из равнобедренных треугольников будет еще и равносторонним.
WBR CrazyElk
P.S. С равнобедренным тоже “не все чисто”. Замкнутая непрерываная кривая может строится и по принципу фрактала причем нобязательно ограниченного. Ни конечность периметра ни гладкость или диффиренцируемость изменения растояний между точками при такой “замкнутой кривой” не гарантируется. А фактически при рассмотрении доказательства о возможности построения равнобедренного (в том виде как изложено) неявно обращаются к параметрическому представлению кривой и используют непрерывость функции расстояний между точками в зависимости от параметра t. Вот насчет непрерывности функции расстояния для “извращенных случаев” я не уверен . Так что по гамбурскому счету даже расуждения о равноберенном треугольнике не вполне строги.
при сторонах квадрата стремящихся к нулю, почему бы и нет?
Это не понял. Например на куске прямой, как взять 4 точки чтобы получился (маленький) квадрат?
“Пример”
Да, не так просто как я думал…
P.S. С равнобедренным тоже “не все чисто”. Замкнутая непрерываная кривая может строится и по принципу фрактала
Попрошу не выражаться! (под “замкнутой кривой” я имел ввиду непрерывную иммерсию окружности в плоскость:P)
Но кажется в такой форме не так просто доказать. Хотя проблема по-моему только в 1-ом пункте. То есть достаточно изначально найти такую точку А чтобы для близкой точки В построился равнобедренный треугольник
АВС с АС>АВ. Думаю знаю как, но муторно об’яснять… (Для гладкой кривой проблем нет)
Но кроме этого пункта проблем не вижу -дальше все по плану!
п.с. Прошу прощения за вульгаризмы, но видит бог - не я начал!😁
п.п.с (для CrazyElk) Должно быть “правильное” доказательство (что на трехмерном торе графики 3х функций специального вида пересекаются в некоторой точке), но я его не могу придумать
Да, не так просто как я думал…
Выразите сторону(её длину) правильного треугольника через диаметр описанной окружности, вот вам и решение Вашей задачи.
…или новая задача… 😉
Для квадрата, то же самое
Думаю, этой задачки-загадки ещё не было
Плывет по океану корабль - тюрьма с заключенными. Капитан корабля - начальник тюрьмы. Что-то ему привиделось, что грядёт шторм. Ну он и говорит всем: “Заключенные, кто спасёт мне жизнь - тому я выполню любое его желание”
Ну и как полагается, случается шторм и все Заключенные погибают, кроме одного. Этот один спасает капитана, спасает ему жизнь. Их выбрасывает на берег. И вот сидят они на песке.
-Ты спас мне жизнь, а я - человек слова. Говори своё одно желание
-капитан, у меня пожизненный срок. Сократи мне его ровно в два раза
Капитан подумал поразмышлял и сократил
Как он это сделал?))
Выразите сторону(её длину) правильного треугольника через диаметр описанной окружности, вот вам и решение Вашей задачи.
В смысле.
Ну выразим мы длинну стороны треугольника через диаметр описанной окружности D*sin60 - что это дает в плане доказателства?
А давайте рассмотрим в качестве “примера” замкнутой кривой “кривую Пеано” замыкая ее по нижней стороне квадрата. 😃
Выразите сторону(её длину) правильного треугольника через диаметр
В смысле алгоритм
На кривой есть точка А с координатами Х, У.
Требуется найти точку В (Х2,Y2) и С(X3, Y3) , что бы расстояния между точками А, В, С было идентичным
На кривой есть точка А с координатами Х, У.
Я привел конкретную кривую и конкретную точку А на ней такую что при любом выборе двух других точек В и С на этой кривой равносторонего треугольника не получится.
Это доказывает что не для любой точки на кривой можно построить равносторонний треугольник такой что одна из вершины лежат в заданной точке, а две другие на этой же кривой.
Но требуется доказать что на любой замкнутой кривой найдутся три такие точки что они образуют равносторонний треугольник (возможно с некотрыми дополнительными ограничениями относительно ограниченности и гладкости этой кривой).
Как он это сделал?))
Погуглил и нашел ответ на загадку под названием “Пожизненное заключение”
Неужто уже все придумано до нас?..вот в чем вопрос…