Балансир для лопастей?
Действительно так. Всё, буду искать то который KOV показал.
Отношение расстояний от оси вращения до центров масс лопастей после перестановки лопастей с балансира на ротор перестает соблюдаться.
? Это как может перестать соблюдаться отношение, если задача балансировки - вывести центры масс в одно место при одинаковой массе лопастей ?
Хоть на метр отодвигайте… тем самым только увеличив чувствительность (плечё на силу) на дизбаланс, но “отношение” никуда не денется.
? Это как может перестать соблюдаться отношение, если задача балансировки - вывести центры масс в одно место при одинаковой массе лопастей ?
Хоть на метр отодвигайте… тем самым только увеличив чувствительность (плечё на силу) на дизбаланс, но “отношение” никуда не денется.
Не обязательно даже центры масс должны быть в одном месте и масса одинакова. Можно сделать вращающуюся конструкцию с грузом 0.5кг на расстоянии 1м от точки вращения и грузом 1кг на расстоянии 0.5м на противоположной стороне и крутится она будет отлично.
? Это как может перестать соблюдаться отношение, если задача балансировки - вывести центры масс в одно место при одинаковой массе лопастей ?
Хоть на метр отодвигайте… тем самым только увеличив чувствительность (плечё на силу) на дизбаланс, но “отношение” никуда не денется.
Это идеальный случай, но далеко не всегда оправданный. Иногда попадаются вообще казусы такого рода: лопасть 1 легче, но перетягивает качели вниз. Какую лопасть тогда утяжелять? Можно обе, конечно, но количество наклеенного может не обрадовать. Так что вполне оправданно плюнуть на массы лопастей и только уравновесить качели. В таком случае в статике будет соблюдаться отношение m1*r1 = m2*r2 (так как крутящие моменты m1*g*r1 и m2*g*r2 равны) и лопасти будут уравновешены даже при разных массах. В динамике к ним добавится центробежные силы которые равны m1*r1*w^2 и m2*r2*w^2 (где w - угловая скорость равная для обеих лопастей). Как видно из формул они тоже будут уравновешены коль m1*r1 и m2*r2 равны. В итоге разница масс будет влиять лишь на мелкие нюансы вроде различия сил инерции препятствующих кручению лопастей вдоль продольной оси (циклический шаг). Учитывая что балансировку вдоль продольной оси вообще фиг проведешь, на подобные мелочи можно просто забить.
… В таком случае в статике будет соблюдаться отношение m1*r1 = m2*r2 и лопасти будут уравновешены даже при разных массах. В динамике к ним добавится центробежные силы которые равны m1*r1*w^2 и m2*r2*w^2 (где w - угловая скорость равная для обеих лопастей). Как видно из формул они тоже будут уравновешены коль m1*r1 и m2*r2 равны.
Вы немного путаете массу лопасти (как протяжённого тела), и массу лопасти приведённую для простоты к её центру массы. (то - что вы подставили в уравнение).
В Вашем случае (массы не равны, но лопасти уравновешены на балансире) - для второго утверждения, о равенстве моментов центров масс, нет ровным счётом никакого основания. Если веса разные - значит и расстояния до центра массы разные, то есть разные и m и r (такие, что дадут равенство произведений). Следовательно - никакого динамического баланса на самом деле нет. Ко всему прочему есть ещё и статический (просто по весу) дисбаланс.
Только при условии равенства веса и одновременном равенстве моментов - будет балансировка. Так как в этом случае - совпадают расстояния до центров масс.
Угу, поэтому лопасти балансируются в два шага - сначала центры масс приводятся в одну точку, как правило - добавлением скотча на один из концов одной из лопастей.
А на втором шаге уравновешиваются качели, путем добавление скотча в центр масс более легкой лопасти.
Вы немного путаете массу лопасти (как протяжённого тела), и массу лопасти приведённую для простоты к её центру массы. (то - что вы подставили в уравнение).
В Вашем случае (массы не равны, но лопасти уравновешены на балансире) - для второго утверждения, о равенстве моментов центров масс, нет ровным счётом никакого основания.
Есть. Чтобы не скатываться к интегралам от функции распределения массы вдоль лопасти (нас просто застрелят тут 😃 ) рассмотрим каждую лопасть как систему из множества N точечных масс находящихся на различных расстояниях от центра вращения. Крутящий момент создаваемый такой лопастью будет равен сумме элементарных моментов, т.е.
(g*m(1)*r(1)+g*m(2)*r(2)+…g*m(N)*r(N)) или, что тоже самое, g*(m(1)*r(1)+m(2)*r(2)+…m(N)*r(N)). При уравновешенном балансире мы получаем равные крутящие моменты для обеих лопастей и равенство суммы произведений масса*плечо для каждой лопасти:
m1(1)*r1(1)+m1(2)*r1(2)+…m1(N)*r1(N) = m2(1)*r2(1)+m2(2)*r2(2)+…m2(N)*r2(N)
центробежные силы действующие на данную систему будут равны сумме элементарных сил (поскольку вектора сил параллельны и однонаправленны):
(m(1)*r(1)*w^2+m(2)*r(2)*w^2+…m(N)*r(N)*w^2) или, что тоже самое, w^2*(m(1)*r(1)+m(2)*r(2)+…m(N)*r(N))
Квадрат угловой скорости выносится за скобки т.к. угловая скорость всех точек равна. В итоге имеем соблюдающееся равенство:
w^2*(m1(1)*r1(1)+m1(2)*r1(2)+…m1(N)*r1(N)) = w^2*(m2(1)*r2(1)+m2(2)*r2(2)+…m2(N)*r2(N))
то есть центробежные силы уравновешены для данной системы вне зависимости от того, как распределяется масса между элементарными частями и вне зависимости от их количества.
P.S. Какой бы балансир вы не выбрали и как не играли с центрами масс - это все статическая балансировка. Динамическая по самому определению выполняется раскруткой до рабочих оборотов. Динамический дисбаланс характерный для валов (вспомните динамическую балансировку валов или автомобильных колес) у вертолетного ротора практически отсутствует в силу очень малой толщины лопасти по сравнению с ее длиной. Хотя в динамике балансировка все же может нарушаться из-за различий в деформации лопастей под нагрузкой. Но тут попытки выровнять массы лопастей никак не помогут, а регулировать модуль упругости готовой лопасти не представляется возможным. Да и растягивание лопастей, на мой взгляд, весьма невелико.
P.P.S. Вопрос оказывается уже возникал. И ответ был rcopen.com/forum/f19/topic5565/7
Хотя в динамике балансировка все же может нарушаться из-за различий в деформации лопастей под нагрузкой. Но тут попытки выровнять массы лопастей никак не помогут…
?? Почему же? На лопасти по мимо центробежной силы (влияющей на “элементарный” дисбаланс) действует ещё масса других:
1 - поворачивающий (в цапфе) момент индуктивного сопротивления лопасти(компенсируемый центробежной силой - а если радиусы центров масс разные - значит и результирующая сила и поворот - будут разные, что приведёт к нарушению аэродинамического равновесия при не нулевом угле атаки)
2 - моменты подьёмной силы (при циклических шагах) на лопастях
Вот тут то, и “вылазит” несоответствие центров масс.
Так как при равных моментах (интегрально) скажем по подьёмной силе, мы будем иметь разные моменты от вертикальных движений лопасти (в силу несовпадения радиусов центров масс).
Если бы мы говорили о балансировке колеса, то да - вес одного никак не соотносится с весом другого. У них и “подвесы” фактически разные и движение чисто радиальное.
P.S. - Ну да, по ссылке об этом и речь…
Во первых, подобное смотрится довольно смешно и странно. Вы предполагаете, что производитель лопастей не сумел добиться идентичного расположения центров масс, однако добился точного расположения центров давления, причем при разных углах атаки лопасти (п.1) и точного соответствия модуля упругости лопастей по всей длине (п.2)?
Да, кстати, я и в примере 1 могу показать, что расположение центра масс почти не играет роли. “Почти” это потому что центр вращения лопасти в цапфе все таки не совпадает с центром вращения ОР, но это влияние невелико. Приводить эпюры и формулы?
А с примером 2 еще веселее. Как только мы перестаем рассматривать лопасть как одномерный предмет (отрезок) с распределенной массой, а предполагаем что лопасть изгибается (в общем-то так оно и есть), то дисбаланс легко наступает даже в случае если центры масс выровнены! То есть центры масс совпадают, упругость лопастей одна и та же, геометрия идентична… а дисбаланс присутствует. К счастью это все тоже все невелико если мы, конечно, не рассматриваем патологические случаи типа “одна лопасть из чугуна, другая из бальсы”.
P.S. Летаю на лопастях выровненных только по балансиру. По массе они немного отличаются. В висении и плоском полете вибрации никакой нет. Про поведение в хитрых манёврах не скажу - т.к. не умею.
Во первых, подобное смотрится довольно смешно и странно. Вы предполагаете, что производитель лопастей не сумел добиться идентичного расположения центров масс, однако добился точного расположения центров давления, причем при разных углах атаки лопасти (п.1) и точного соответствия модуля упругости лопастей по всей длине (п.2)?
Я не предполагаю, а уверен. Так как лопасти делаются по одной матрице (если карбон) определяющей геометрию. Или по одной программе CNC (если дерево). А вот смола, имеет свойство неравномерно распределяться с внутреней стороны 😈 Что и приводит к разбалансировке. И дерево - не однородно по плотности.
P.S. Летаю на лопастях выровненных только по балансиру. По массе они немного отличаются. В висении и плоском полете вибрации никакой нет. Про поведение в хитрых манёврах не скажу - т.к. не умею.
Я могу “невидеть” когда у меня вал межлопасной раскручивается, ну и что? Что от этого меняется - вижу или нет?
Ещё раз. Если бы лопасть двигалась только по окружности - вопросов нет! Балансируйте так.
Но у лопасти, кроме центра массы по длинне, есть ещё (должно быть) определённое расположение ц.м. по хорде, влияющее на её свойства.
Всё несколько сложнее, чем кажется на первый взгляд.
Делайте как нравиться, если такого рода “упрощение” считаете нужным. Ваш личный выбор. Но зачем - советовать это другим?
Делайте как нравиться, если такого рода “упрощение” считаете нужным. Ваш личный выбор. Но зачем - советовать это другим?
На сем дискуссию заканчиваю как превратившуюся в персональный наезд и потерявшую смысл. Я вам конкретику, а Вы мне туман какой-то про “определенное положение” и “всё несколько сложнее”, да еще и обвинения в распространении ереси теперь пошли. Делайте как привыкли, это Ваш личный выбор.
Наезд? 😁 Это ж кто на кого наезжает, ещё разобраться надо. 😃
А какую конкретику Вы хотите? Что в Вашем варианте не совпадают плечи сил? Так это, лично для меня - очевидно. И последствия - очевидны. Всё зависит от “степени” разбалансированности, не более того.
Вы предлагаете мне рисовать для Вас картинки и что то доказывать?
Честно говоря, не вижу причин это делать. Хотите, нарисуте сами векторы и посмотрите на результаты.
Вибрация это же что такое? Если трясёт верт на сантиметр, то вибрация! А если на 5мм - то нет? А на 1мм ? 😃 А на 0.5 … ?
Где та граница, которая Вас убеждает в её отсутствии? Может, стоит таки - взять и отбалансировав лопасти полностью - сравнить? Может будет лучше? (уж точно не хуже!)
Предложеный “дедовский” способ балансировки центров масс - это максимум из того что доступно “подручными средствами”. ИМХО, потратить 5 минут времени и 5 - 10 см скоча для уверенности в результате, мне кажется ОЧЕНЬ низка цена.
А смысл в том, что кроме меня и Вас, этот топик читает куча народа, люди начинающие, возможно - плохо разбирающиеся в “плечах” и “массах”.
А Ваше утверждение о “неважности” полной балансировки, кем то может быть воспринято слишком буквально.
И что будет…?
По-моему спор ни о чем. И дураку понятно, что идеальная балансировка - когда одинаковы геометрия(что на совести производителя), вес и расположение центра масс по размаху и хорде. Так вот к этому и надо стремиться. А балансировка при помощи только весов - самообман.Так что AlexSr прав на 100%!
По-моему спор ни о чем. И дураку понятно, что идеальная балансировка - когда одинаковы геометрия(что на совести производителя), вес и расположение центра масс по размаху и хорде. Так вот к этому и надо стремиться. А балансировка при помощи только весов - самообман.Так что AlexSr прав на 100%!
Товарищ, Вы вообще о чем? Во-первых, не надо путать балансировку с симметричностью. Понятно, что симметричная система будет сбалансированной, но это частный случай. А во-вторых, кто тут говорит о балансировке с помощью весов? Наоборот, я говорю о том, что отбалансировав лопасти на “качалке”, добавлением скотча лишь на кончик одной лопасти, можно добиться хорошей балансировки. То есть можно обойтись без весов и без иных способов приведения центров масс к одному радиусу. Условия: у балансира между точками крепления лопастей расстояние такое же как и на ОР вертолета, типовые разбросы масс лопастей (не более единиц процентов). Понятие “хорошей балансировки” сформулировать трудно… скажем так, это когда разница пилотом без подсказки не ощущается.
P.S. А “дураку понятно” это хорошо подмечено. Завидую я им, им всегда все понятно.
У меня просьба многоуважаемым гуру - вместо спора написать четкую методику по балансировке - шаг за шагом. Я думаю многие новички будут признательны
У меня просьба многоуважаемым гуру - вместо спора написать четкую методику по балансировке - шаг за шагом. Я думаю многие новички будут признательны
- Зарегистрируйтесь на Хелифрике
- Скачайте видео из этой темы, в частности - балансировка лопастей
PS Можно смотреть без звука, все и так понятно.
вот в этом балансире есть косяк небольшой. красные ножки хоть и на подшипниках по уму, но болтаются на только в одной плоскости. в результате когда прикручиваешь туды тяжёлую лопасть ножки можно нечаянно сдвинуть под другим углом - и падает точность балансировки.
но на самом деле это проблема не страшная) - просто в края этих ножек между ними надо вставить 2 распорки - и тогда они перестанут болтаться 😃 да и так если акуратно - то вполне сойдёт ) тут уже сказано чтонеровности стола - так же как и смещение ножек которое приводит к нероности установки - не сильно влияет. но всё же…
надеюсь внятно изложил мысль 😃
2 sapa1 Вы вдумайтесь, о чем говорите! Как можно обойтись без весов? Поясню на примере. Вспомните старинный прибор - безмен.На одном плече висит взвешиваемый предмет, скажем 1 кг. А на другом плече - в 10 раз большем - гирька весом 100гр. И система уравновешена! А вес отличается в 10 раз! А уравновешена потому, что центры масс на разных радиусах. Вы так предлагаете балансировать лопасти? Как правильно делать - коротко и ясно сказал М.С. P.S. Расстояние между точками крепления лопастей не имеет значения для балансировки - было бы одинаковым.
Вспомните старинный прибор - безмен.На одном плече висит взвешиваемый предмет, скажем 1 кг. А на другом плече - в 10 раз большем - гирька весом 100гр. И система уравновешена! А вес отличается в 10 раз! А уравновешена потому, что центры масс на разных радиусах.
Совершенно согласен с Вами, коллега. 😃 Только вот кто сказал, что наша задача уравнять веса? Наша задача избавиться от вибраций, то есть максимально скомпенсировать силы вызывающие данные вибрации. Простейший способ это сделать систему идеально симметричную относительно оси вращения, но способ не единственный. Раз уж вы приводите аналогии с безменом, то и я парочку приведу, хорошо? Возьмите для примера коленчатый вал одноцилиндрового двигателя внутреннего сгорания и посмотрите на балансировку:
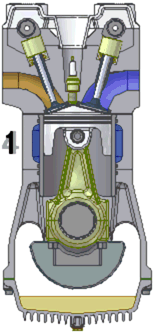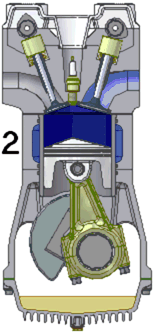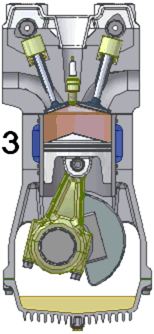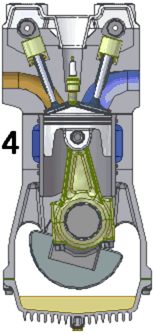
или на устройство центрифуги в Звездном городке:

Это примеры того, как сбалансированы несимметричные системы. Распределение масс по разные стороны от оси вращения отличается, но силы уравновешены. На практике подобная балансировка оказывается хуже симметричной. Ведь есть еще силы инерции второго (и более) порядка, например при возвратно-поступательном движении упругих лопастей и дисбаланс возникающий вследствие упругой деформации несимметрично отбалансированного ротора. Но эти силы значительно меньше сил первого порядка.
А теперь еще раз прослушайте что я утверждаю: иногда лучше отбалансировать ротор без выравнивания масс лопастей, чем мотать слишком много скотча для “традиционного” выравнивания. Выгоды от симметричности развесовки могут оказаться незаметными в сравнении с ухудшением аэродинамики лопастей и общим увеличением массы ротора. (Кстати, “традиционная” балансировка тоже не симметричная, она приводит к одной окружности лишь центры масс лопастей, но не распределение масс вдоль лопасти - так что вибрации и тут неизбежны.)
P.S. Кстати, вопрос всем, а с какой точностью вы подбираете вес необходимого балансировочного скотча - можете оценить? Ну хотя бы ориентировочно - 20%, 10%, 5% или 1%.
а какой смысл в процентах? Ведь дисбаланс меряется в г*мм*градус, вроде как
или это процент от массы лопасти? так это от пары лопастей зависит…
И если лопасть 100гр, то скотча может быть и меньше грамма, но чаще в пределах 5-ти грамм. А если лопасть 13 грамм… ну, дома таких весов нет, не скажу…
Вес лопастей на 600n - порядка 120 -130 грамм. Точность взвешивания - 0.1 грамма.
При весе лопастей до 100 грамм, точность (другие весы) 0.01 грамма.😉
Так что, по любому не больше 0.1% .
